Rpn Calculator Exercises

Overview

These instructions give further details on a set of exercises in a github repo.

That repo is to practice different kinds of code refactorings. There are several exercises, each of which starts at a git tag in the repo.

The tags for this repo are:

00-project-start
01-wrap-collection-start
01-wrap-collection-end
02-open-closed-start
02-open-closed-end
03-strategy-pattern-start
03-strategy-pattern-end
04-factory-pattern-start
04-factory-pattern-end
05-template-method-start
05-template-method-end
06-composite-object-start
06-composite-object-end

After cloaning, you can confirm this list by using git (not the order will be different from what is listed above):

git tag -l

Working with the repo

You will need to install a few things for this to work. Have a look here. Note, you will not need gradle installed as described there.

In addition, you probably want to install some IDE. Any of these will be fine:

Once you have a command line, git, and an IDE, you are ready to:

the repo (do this once)
Select an exercise and work on it
Move to the next exercise to either review one possible solution or start another exercise

Cloning Repo

Clone this project as usual and review the tags:

git clone https://github.com/schuchert/rpn_exercises.git
cd rpn_exercises
git tag -l

Select an exercise

In the repo directory, use git branch with a tag to create a branch based on one of the exercises, i.e.,

git checkout -b <new_branch_name> <tag_name>

For example, to work on the (recommended) first exercise:

git checkout -b wrap-collection-exercise 01-wrap-collection-start

You can now make commits to this branch as you normally would use git.

Once you are done, you can compare your results to master, which has one possible solution to the problem presented in the exercise.

Before doing that, commit any changes you want to keep in the branch created for this exercise.

Currenntly Clean

Verify you are clean before comparing or switching to a different exercise.

git status
On branch wrap-collections-exercise
nothing to commit, working tree clean

Compare to one possible solution

Assuming your changes are committed and you are in the branch you created to work on the 01-wrap-collections-start tag, you can compare your changes to master:

git diff 01-wrap-collections-end

Switch to tag

When your repo is clean and you’ve reviewed your results against master, you can start a new exercise by following the steps in the select an exercise above above.

Wrap Collection

Get Started

git checkout -b wrap-collection-exercise 01-wrap-collection-start

Background

An actual HP Rpn Calculator never runs out of values. If your regular Java stack runs out of values, using pop() or peak() throws an exception. This makes the Java Stack abstraction different from the needs of your domain. This makes using it directly a possible (actual in this case) voilation of the Dependency Inversion Principle.

Goal

We want to make our stack never empty. Technically the value returned should reflect the so-called T register. We will simplify this and instead return 0 when all the user-entered values are gone. (See Rpn Description for too much detail.)

Wrap Collection Hints

    	--- title: Wrap Collection Hints ---

Introduce a new class, RpnStack. This class will wrap the Stack<BigDecimal>. Then update the RpnCalculator to use this new class.

You will need to have a few methods in your RpnStack class:

push
pop
peek
size

Make sure you initialize your collection of values in the constructor of RpnStack.

Also make sure to remove the Stack<BigDecimal> from the RpnCalculator class.

Check

When you’ve commited all your changes:

git diff 01-wrap-collection-end

Open Closed Principle

Get Started

git checkout -b open-closed-exercise 02-open-closed-start

Background

The interface to the calculator changes every time you add a new operator. This violates the Open/Closed Principle Experiment with making a change to the API and get the code to pass.

Goals

Adding a new operator does not change the interface to the calculator
All exisitng operators use the new approache
The number of methods on the classs is significantly reduced
Introduce some negative testing to make sure use of the new API produces “reasonable” errors

Open/Closed Hints

    	--- title: Open/Closed Exercise Hints ---

Example of before/after test

The tests will all be converted to using the new API of the calculator. One way to do that is below in the after example.

Test Example Before Applying OCP

    @Test
    public void addsNumbersCorrectly() {
        calculator.enter(BigDecimal.valueOf(13));
        calculator.enter(BigDecimal.valueOf(-2));
        calculator.add();
        assertEquals(BigDecimal.valueOf(11), calculator.x());
    }

Test Example After Applying OCP

    @Test
    public void addsNumbersCorrectly() {
        calculator.enter(BigDecimal.valueOf(13));
        calculator.enter(BigDecimal.valueOf(-2));
        calculator.execute("add");
        assertEquals(BigDecimal.valueOf(11), calculator.x());
    }

Notice, you can do this in small steps. Assuming adding execute(String), you could:

Update addsNumbersCorrectly to call a new, as yet undefined method.
- Another reasonable apporach is to create a new test rather than change an exsiting test
Add the missing method
The first version simply calls the add method:

public void execute(String operatorName) {
    add();
}

Find other tests that use the add() method and update them to instead call execute("add")
Update another operator, say subtract.
Update the execute method:

public void execute(String operatorName) {
    if("add".equals(operatorName))
        add();
    if("subtract".equqls(operatorName))
        subtract();
}

Update all uses of the subtract() method.
Continue until none of the named operator methods are used in the test.
Make those named operator methods private to confirm they are no longer used.

Example of test for unknown operators

Every solution introduces problems. The change in the API of the RpnCalculator introduces a few issues:

We’ve replaced compile-time checking with either no checking or runtime checking
A simple error like Add versus add might be hard to notice

While this is not “the final” version, we can begin to address some of these things with some tests. Here’s one such test that at least addresses mis-named operators.

    @Test
    public void handlesUnknownOperator() {
        String badOperatorName = "--BOGUS--";

        IllegalArgumentException illegalArgumentException = assertThrows(
                IllegalArgumentException.class,
                () -> calculator.execute(badOperatorName)
        );

        assertEquals("Operator: '" + badOperatorName + "' does not exist", illegalArgumentException.getMessage());
    }

Check

When you’ve commited all your changes:

git diff 02-open-closed-end

Strategy Pattern

Get Started

git checkout -b strategy-pattern-exercise 03-strategy-pattern-start

Background

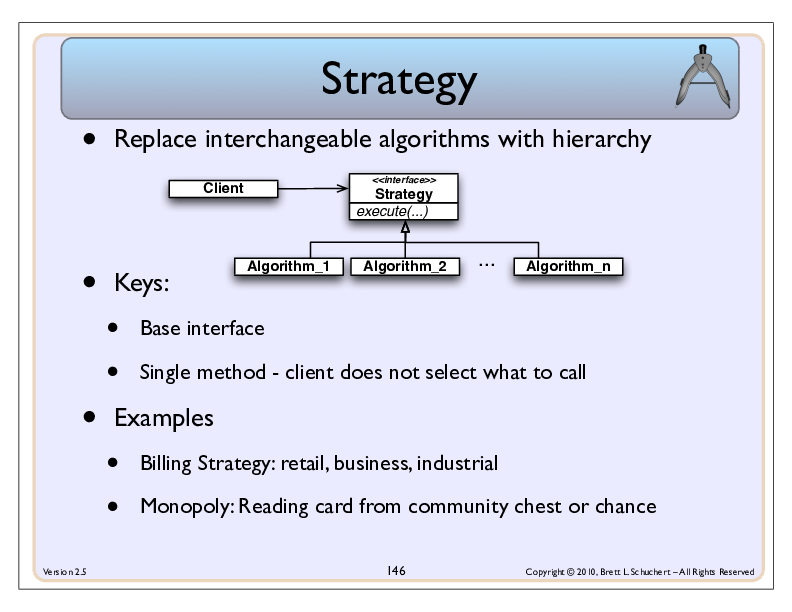
All of the operators look similar. Rather than writing each as its own function, we can do the same thing as a class. Note: With Java 8 we could also use Lambdas, but for now let’s take more of a traditional approach to the Stragegy Pattern. Image of Stragegy Pattern

Goals

We want to define an interface with a single method that will work all of the operators. Review each of the operators, and determine what, if anything, is common across all operators.

Once you’ve done that, create an appropraite interface, have each of the functions in its own class, which implements that interface.

Update the solution from calling a bunch of functions to instead using instances of the various subclasses of your new interface.

Strategy Pattern Hints

    	--- title: Strategy Pattern Hints ---

There are several things woth noticing about what is common and what is not common:

Some operators take 2 parameters, e.g., add
Some operators take 1 parameter, e.g., factorial
Currently all operators return a value, given what you know about calculators, is that a safe assumption?
- Hint, it is not. We will eventually have operatos like swap that reverse the top two values, or drop that simply gets rid of a values
Eventually there might be operators that consume no values but actually put values on the stack, e.g., random

About the only thing that will ultimately be common across all of the math operators will be that they:

consume 0 or more operands
produce 0 or more results

So the only thing that all of the operators have in common will be the RpnStack.

Check

When you’ve commited all your changes:

git diff 03-strategy-pattern-end

Factory Pattern

Get Started

git checkout -b factory-pattern-exercise 04-factory-pattern-start

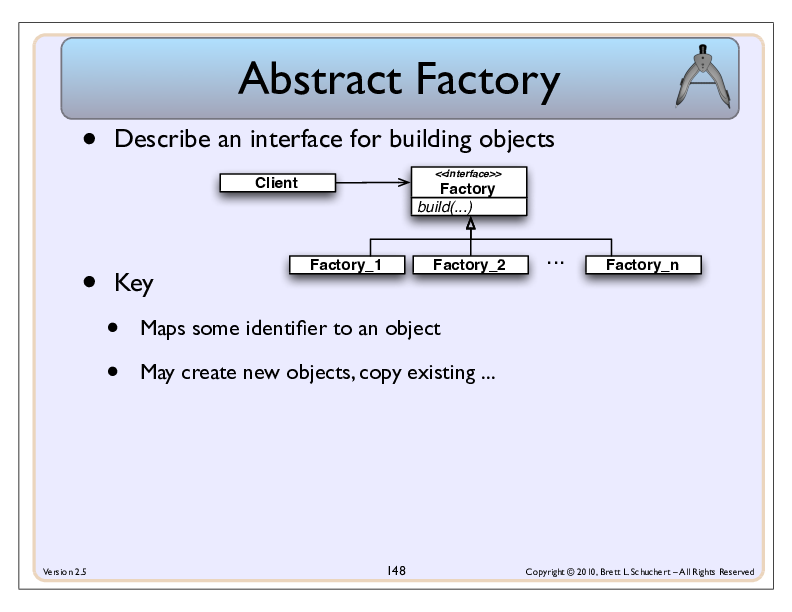
Background

Image of Abstract Factory

Goals

There’s an abundance of code in the RpnCalculator that can be put into its own class.

Factory Pattern Hints

    	--- title: Factory Method Exercise Hints ---

The eecute method in RpnCalculator violates the Single Responsibility Principle. It does different things that change for different reasons.

Locate an operator given a name, e.g., add, factorial Or provide a reasonable error if not found
Execute the found operator

Breaking these two things into separate responsibilities, e.g., methods, cleans up the code.

Once you’ve made this improvement, a next step might be to pull the location responsibility into its own class.

This becomes a factory for operators. The RpnCalculator deletages the lookup of a operator name to the factory, then sends execute to an operator.

For this to work easily, it helps that we’ve already introduced the Strategy Pattern in the from of a Operator interface.

A good end result for RpnCalculator::execute could be:

public void execute(String operatorName) {
    Operator op = factory.operatorFor(operatorName);
    op.execute(values);
}

Things to do:

Initially re-write the excute method to separate lookup from execution.
Extract lookup into its own method
Create a new class called `OperatorFactory
- It is possible to move the lookup method with refactoring tools
The OperatorFactory holds the Map<String, Operator> field
The factory pre-poulate the map with all of the operators
Replace the map field in RpnCalculator with the an instance of OperatorFactory
Re-write the execute method to use the factory and execute the method as shown above

As a bonus, you can use a library like Class Graph to dynamically find the classes. Later versions of this project do that.

Check

When you’ve commited all your changes:

git diff 04-factory-pattern-end

Template Method Pattern

Get Started

git checkout -b template-method-exercise 05-tempalte-method-start

Backgound

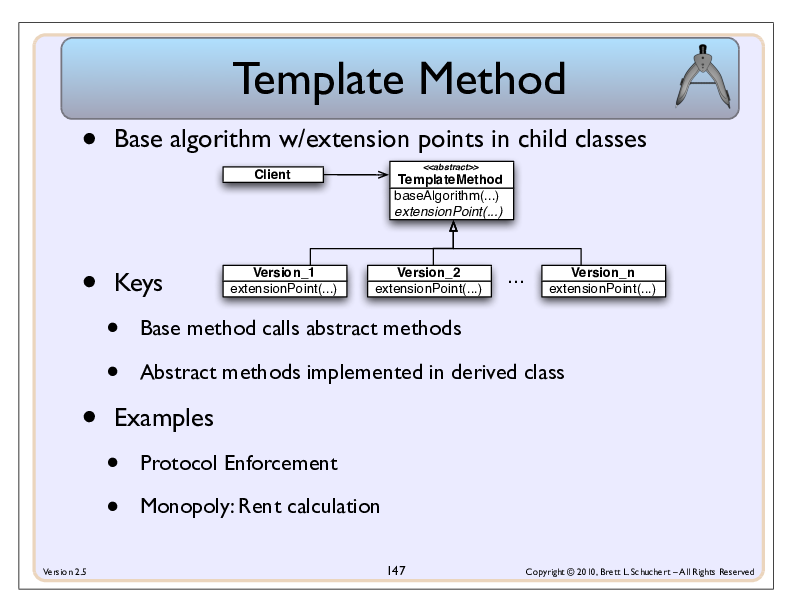
There’s quite a bit of duplication in all of the binary operators. Consider add versus subtract:

add	subtract
`BigDecimal rhs = values.pop();`	`BigDecimal rhs = values.pop();`
`BigDecimal lhs = values.pop();`	`BigDecimal lhs = values.pop();`
`values.push(lhs.add(rhs));`	`values.push(lhs.subtract(rhs));`

In fact, the only difference is the calculation of the result. The “algorithm” then is:

Acquire operands (lhs and rhs)
Calculate the result (add or subtract)
Store the result (push)

The Template Method Pattern implements an algorithm in a (typically abstract) base class and has one or more extension points (abstarct methods) for derived classes to implement. Those derived classes fill in the details.

Image of Template Method Pattern

Goals

Remove the dupplication between the various binary operator classes.

Template Method Pattern Hints

    	--- title: Template Method Pattern Hints ---

Create an abstract base class called BinaryOperator
It should implement the Operator interface
Copy th method from one of the existing binary operator class, e.g., Add::execute
Put the result calculation it its own step, e.g., calculate(BigDecimal lhs, BigDecimal rhs), as an abstract method
One at a time, change the implementation of the various binary operator classes
- Extend your new abstract base calss
- Remove their execute method
- Implement the calcualte method
- Remove the implementation of the Operator interface
- Check your tests

Example of BinaryOperator

public abstract class BinaryOperator implements Operator {
    @Override
    public void execute(RpnStack values) {
        BigDecimal rhs = values.pop();
        BigDecimal lhs = values.pop();
        
        BigDecimal result = calculate(lhs, rhs);
        
        values.push(result);
    }

    abstract BigDecimal calculate(BigDecimal lhs, BigDecimal rhs);
}

Example of Add

public class Add extends BinaryOperator {
    @Override
    BigDecimal calculate(BigDecimal lhs, BigDecimal rhs) {
        return lhs.add(rhs);
    }
}

Check

git diff 05-template-method-end

Composit Object Pattern

Get Started

git checkout -b composite-object-exercise 06-composite-object-start

Background

We want our calculator to be “programmable.” By that, we can make our own combinariion of existing operators. For example, Pythagorean’s theorem:

\[C^2 = A^2 + B^2\] \[C = sqrt(A^2 + B^2)\]

Given an a,b of (3, 4), we might do something like this with our calculator:

Entry	Values on RpnStack	Who
3	3	user
2	2, 3	user
pow	9	user
4	4, 9	user
2	2, 4, 9	user
pow	16, 9	user
add	25	user
sqrt	5	user

Imagine if we could turn that into a program named Pythagorean:

entry	Values on RpnStack	Who
3	3	User
4	4, 3	user
Pythagorean	5	user

One way to write the program Pythagorean might be:

entry	Values on RpnStack	Who
Pythagorean	4, 3	user
push2	2, 4, 3	Pythagorean
pow	16, 3	Pythagorean
swap	3, 16	Pythagorean
push2	2, 3, 16	Pythagorean
pow	9, 16	Pythagorean
add	25	Pythagorean
sqrt	5	Pythagorean

Image of Composite Pattern

Goals

Composite Object Pattern Hints

    	--- title: Composite Object Pattern Hints ---

The class you create, e.g., Program class implements Operator.
It holds an ordered list of other operators.
When told to execute, it will simply call execte on each of its contained operators.

Check

git diff 06-composite-pattern-end

Overview

Working with the repo

Cloning Repo

Select an exercise

Currenntly Clean

Compare to one possible solution

Switch to tag

Wrap Collection

Get Started

Background

Goal

Check

Open Closed Principle

Get Started

Background

Goals

Check

Strategy Pattern

Get Started

Background

Goals

Check

Factory Pattern

Get Started

Background

Goals

Check

Template Method Pattern

Get Started

Backgound

Goals

Check

Composit Object Pattern

Get Started

Background

Goals

Check

Comments